Hash Trie Implementation and Performance Analysis
Hash tables are ubiquitous in modern programming practices. In the most common case, they allow you to set up a mapping from a set of strings to a set of arbitrary objects.
Hash tables are especially useful when it isn't known ahead of time what the value of the keys will be and also how many entries will be added.
In C++, a hash table implementation is provided by the standard library through the std::unordered_map type. Another implementation with similar functionality based on a search tree is provided by the std::map type.
In plain old C, there is no built-in library or language support for hash maps or another similar data structure.
I've come across an interesting implementation for a data structure that I have not seen discussed in more classical learning resources: the so-called “Hash Trie”.
Performance analysis against built-in C++ types
A benchmark program was devised. The benchmark program loads up the data structure being tested with E distinct key/value entries, then it proceeds to fetch back each entry through the keys, checking the obtained value against the value originally inserted. This process is repeated N times, with a new freshly-allocated container each time.
For a small number of inserted elements (E = 10, 25, 50, 100, 250, 500, 1000), the benchmark runtime (in milliseconds) is shown below in a log-log graph.
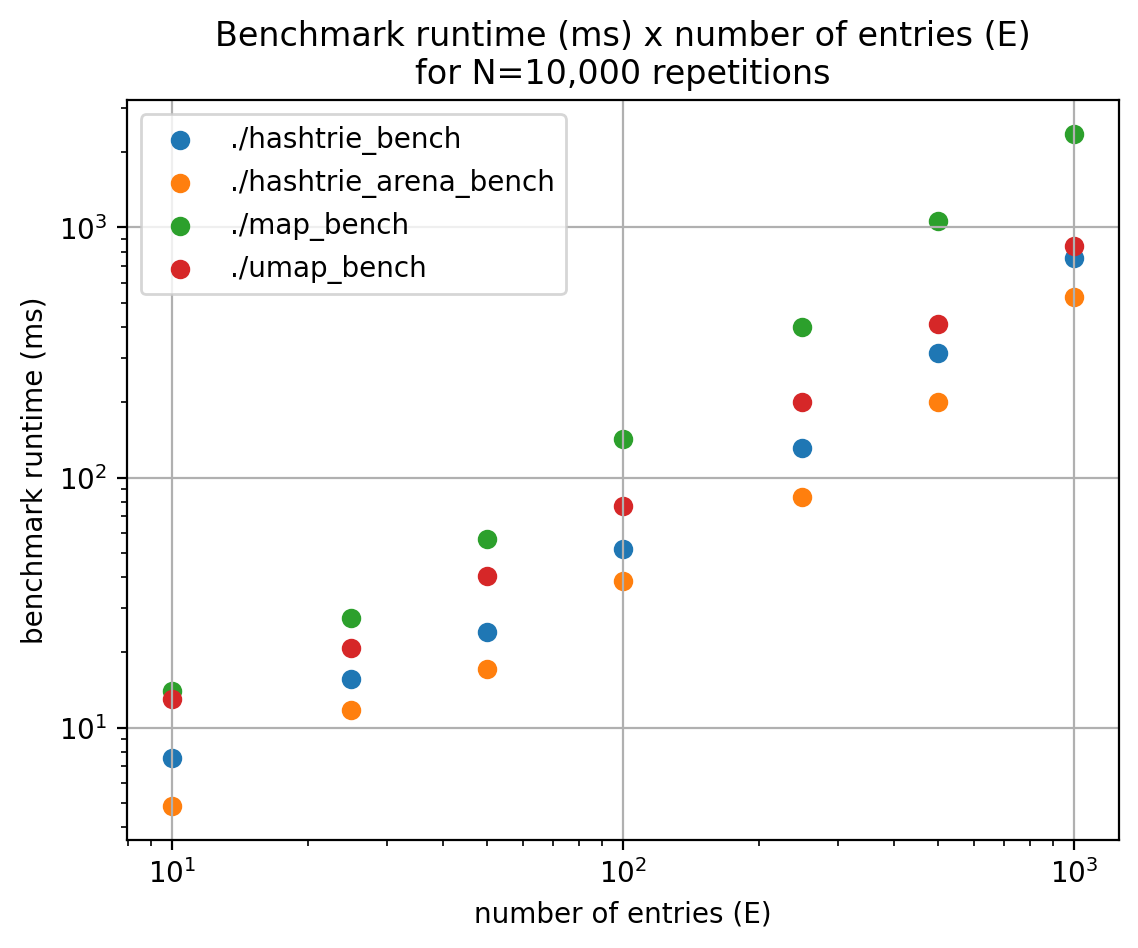
We can see that std::map is consistently the slowest of all, and the trend suggests it has the worst asymptotic behavior.
The second slowest is std::unordered_map (labeled as umap), which presents an initial large overhead for smaller Es.
Then, we have our ad-hoc implementation. Plain hashtrie uses malloc and outperforms both std::map and std::unordered_map for a small number of inserted items, E < 1000.
Finally, by using an allocation arena instead of malloc, the hash trie widens the gap by going even faster.
When looking at larger Es, the obtained benchmark runtime is shown in the graph below:
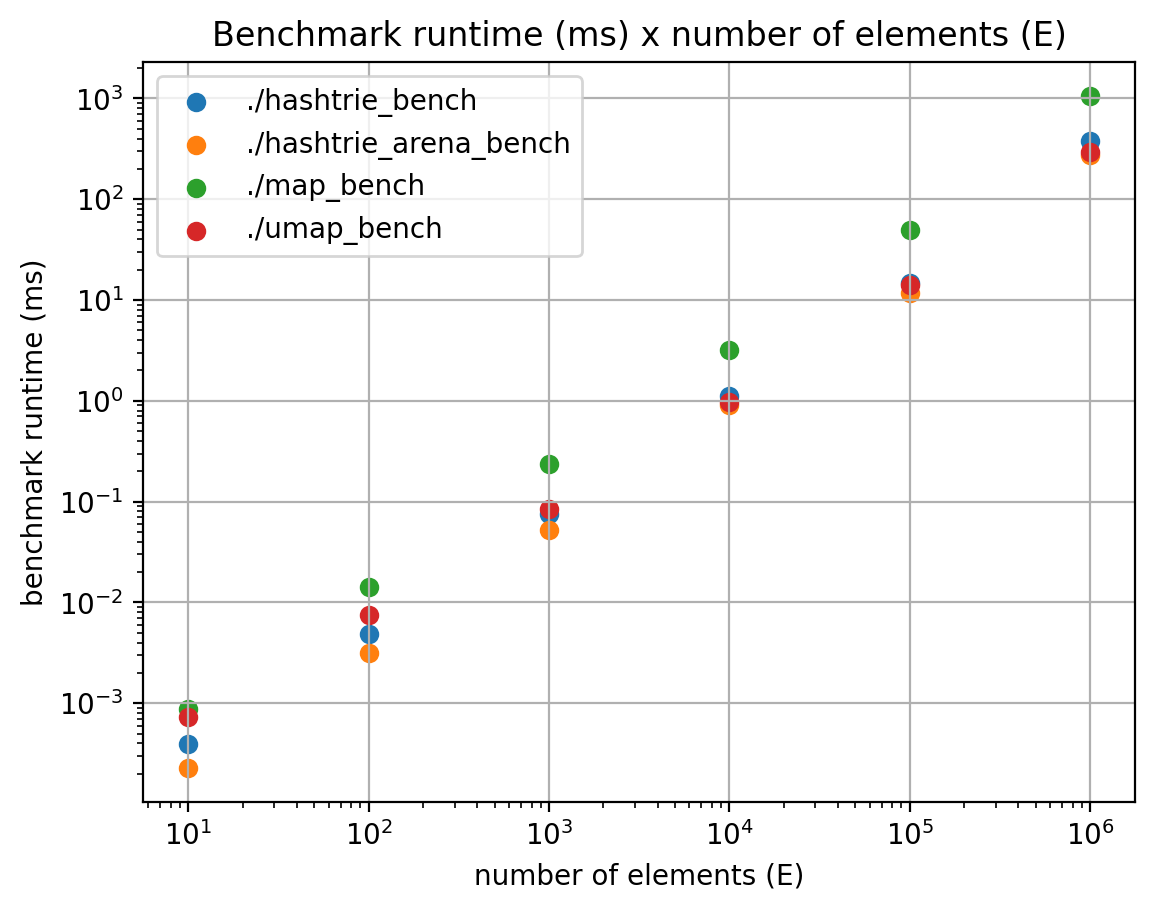
Once again, the previous analysis holds: map seems the slowest, unordered_map the second slowest, and hashtrie_arena is the fastest of the bunch.
Now, looking at the relative runtimes with regard to the faster implementation:
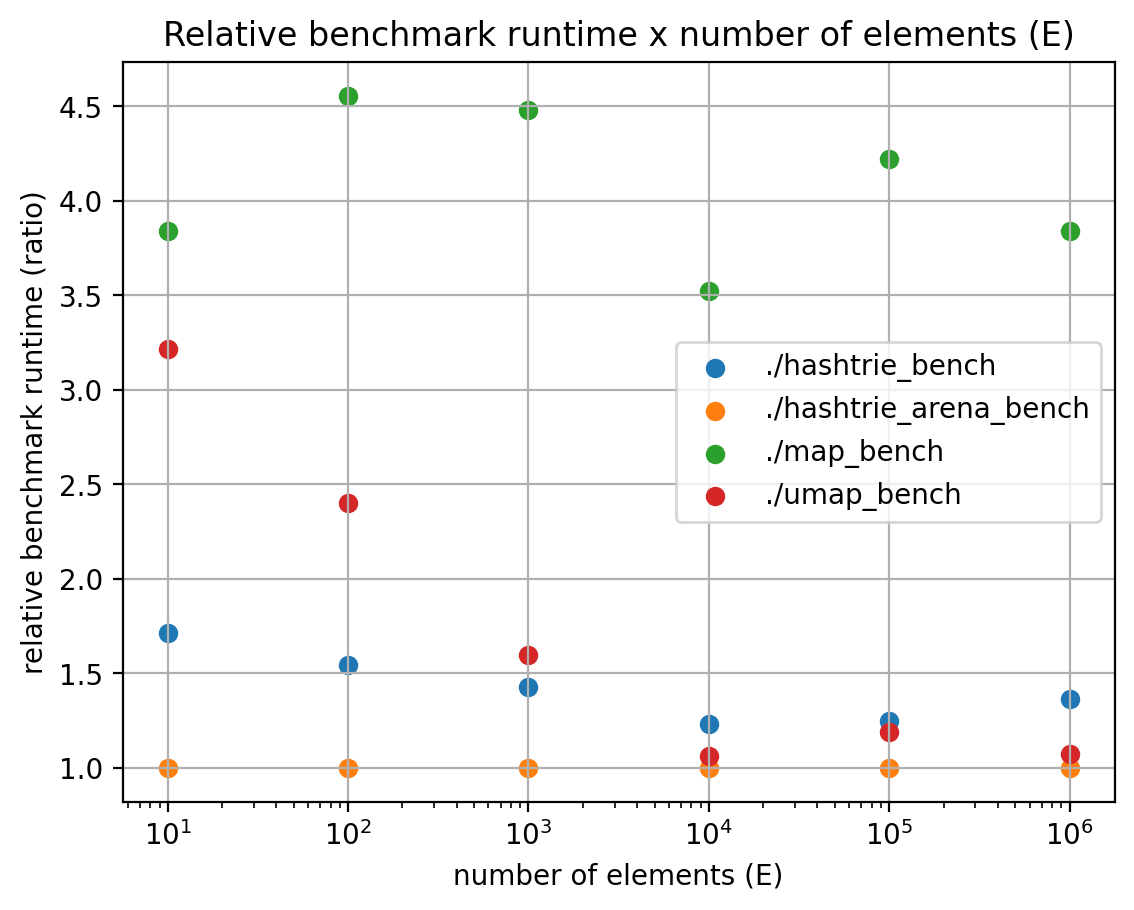
We can see that std::map has a consistent 3x~3.5x slower performance for all the observed E range.
For smaller E, std::unordered_map has a high overhead, relative to a hash trie, but it gets smaller (or is amortized) as E increases.
For larger E, a plain hash trie with malloc() is outperformed by std::unordered_map. Also, we observe that by using malloc() instead of a memory arena, a slowdown of between 25% and 50% is observed in the tested E range, which can be attributed to the C runtime memory allocation overhead.
Finally, by switching the hash trie to an arena-based allocation, the built-in C++ implementations (and the malloc-based hash trie) are all outperformed for the whole range studied.
C implementation
The basic unit of this data structure is a tree node defined as follows:
#define HASHTRIE_CHILDREN 4
typedef struct HashTrie {
struct HashTrie* children[HASHTRIE_CHILDREN];
char* key;
void* value;
} HashTrie;
Note that the above structure is assumed to be initially initialized to all zeroes (thus, all pointers are NULL).
The operation to set a value on the hash trie is as follows:
void hashtrie_set(HashTrie* ht, char* key, void* value) {
assert(ht != NULL);
uint64_t h = hash(key);
HashTrie* p = ht;
while (1) {
if (p->key == NULL) {
p->key = key;
p->value = value;
return;
}
if (strcmp(key, p->key) == 0) {
p->value = value;
return;
}
int cidx = h >> 62;
HashTrie* c = p->children[cidx];
if (c == NULL) {
c = hashtrie_alloc();
p->children[cidx] = c;
}
p = c;
h <<= 2;
}
}
The code to find the entry by its key is very similar:
void* hashtrie_get(HashTrie* ht, char* key) {
assert(ht != NULL);
uint64_t h = hash(key);
HashTrie* p = ht;
while (p != NULL) {
if (p->key == NULL) {
return NULL;
}
if (strcmp(key, p->key) == 0) {
return p->value;
}
int cidx = h >> 62;
p = p->children[cidx];
h <<= 2;
}
return NULL;
}
The following is the hash function suggested by the author I've referenced:
uint64_t hash(char* str) {
assert(str != NULL);
uint64_t h = 0x100;
char* p = str;
while (*p != '\0') {
h ^= *p;
h *= 1111111111111111111u; // 19 ones's
p++;
}
return h;
}
A possible implementation for hashtrie_alloc() function, which returns a newly-allocated and zero-initialized node, is using malloc():
HashTrie* hashtrie_alloc() {
void* p = malloc(sizeof(HashTrie));
if (p == NULL) {
fprintf(stderr, "hashtrie_alloc: out of memory\n");
exit(1);
}
memset(p, 0, sizeof(HashTrie));
return (HashTrie*)p;
}
The faster implementation is using an allocation arena and is described as follows:
#define ARENA_SIZE 10000000
static HashTrie arena[ARENA_SIZE];
static int arena_i = 0;
HashTrie* hashtrie_alloc() {
assert(arena_i < ARENA_SIZE);
HashTrie* p = &arena[arena_i];
arena_i++;
memset(p, 0, sizeof(HashTrie));
return (HashTrie*)p;
}
High-level algorithm
At a high-level, it goes as follows: We start by taking the hash of the key, which is the same as with a hash table. A hash is a single integer number which is deterministically derived by the contents of the key, so that keys with the same contents will have the same hash.
We then check the current node's key. If the current node's key is null, we conclude it is not present anywhere in the hash trie, so we initialize the current node's key and value to the entry we are adding, and we are done.
If the current node has a key, if it matches the key we're looking for, we found the existing entry, we update the value and we are done.
Now, the interesting bit: how we traverse and/or initialize the children. For selecting the child, we use the two highest bits in the hash. Assuming a high-quality or appropriate hash function, each one of the children will be equally likely. We then discard these bits from the hash, so as to use the next 2 bits next time, and keep looking for the key.
This works because, if the key is present in the hash trie, the lookup will traverse the tree in exactly the same manner -- as the hashes will be equal -- eventually finding the key after at most a few steps.
Testing for correctness
The code for the hash trie was tested for correctness with the following program:
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdint.h>
#include "hashtrie.h"
uint64_t walk_acc = 0;
void hashtrie_xor(char* key, void* value) {
uint64_t v = *(uint64_t*)value;
walk_acc ^= v;
}
#define countof(X) (sizeof(X)/sizeof(*(X)))
int main() {
char* strs[] = { "hey", "jude", "don't", "be", "afraid", "take", "a", "sad", "song", "and", "make", "it", "better" };
int len = countof(strs);
uint64_t* vals = (uint64_t*)malloc(len * sizeof(uint64_t));
uint64_t vals_xor = 0;
for (int i = 0; i < len; i++) {
vals[i] = hash(strs[i]);
vals_xor ^= vals[i];
}
HashTrie* ht = hashtrie_alloc();
for (int i = 0; i < len; i++) {
hashtrie_set(ht, strs[i], (void*)&vals[i]);
}
walk_acc = 0;
hashtrie_walk(ht, hashtrie_xor);
assert(walk_acc == vals_xor);
for (int i = 0; i < len; i++) {
void* p = hashtrie_get(ht, strs[i]);
assert(p != NULL);
uint64_t v = *(uint64_t*)p;
assert(v == vals[i]);
}
hashtrie_dump(ht);
printf("All tests passed!\n");
}
Which outputs:
[hey = 0x5558b17792a0]
[don't = 0x5558b17792b0]
[song = 0x5558b17792e0]
[be = 0x5558b17792b8]
[a = 0x5558b17792d0]
[make = 0x5558b17792f0]
[afraid = 0x5558b17792c0]
[jude = 0x5558b17792a8]
[sad = 0x5558b17792d8]
[better = 0x5558b1779300]
[it = 0x5558b17792f8]
[take = 0x5558b17792c8]
[and = 0x5558b17792e8]
All tests passed!
Benchmark program
The various data structures compared were benchmarked with the following program:
#include <assert.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdint.h>
#include "hashtrie.h"
#define RAND_SEED 0x1234
uint64_t rand_next(uint64_t state) {
state *= 1111111111111111111u; // 19 ones's
return state;
}
// volatile prevents optimizations
volatile char** strs;
int main(int argc, char** argv) {
assert(argc == 3);
int str_count = atoi(argv[1]);
int obj_count = atoi(argv[2]);
// initialize benchmark
strs = malloc(str_count * sizeof(char*));
assert(strs != NULL);
uint64_t rand = RAND_SEED;
char buff[50];
for (int i = 0; i < str_count; i++) {
snprintf(buff, sizeof(buff)-1, "%lx", rand);
strs[i] = strdup(buff);
rand = rand_next(rand);
}
for (int t = 0; t < obj_count; t++) {
HashTrie* ht = hashtrie_alloc();
// set
for (int i = 0; i < str_count; i++) {
hashtrie_set(ht, (char*)strs[i], (char*)strs[i]);
}
// get
for (int i = 0; i < str_count; i++) {
void* p = hashtrie_get(ht, (char*)strs[i]);
assert(p != NULL);
assert((char*)p == (char*)strs[i]);
}
}
}